La Incertidumbre y el Riesgo en el Diseño Racional en la Ingeniería Geotécnica (II)

Primera parte en:

La Incertidumbre y el Riesgo en el Diseño Racional en la Ingeniería Geotécnica (I)

La incertidumbre en las propiedades del suelo

La mayoría de los suelos se forma naturalmente en muchos ambientes de depositación diferentes, por lo que sus propiedades físicas pueden variar de un punto a otro. Esta variación puede existir incluso en una unidad de suelo aparentemente homogénea. La variabilidad de las propiedades del suelo es un importante contribuyente a la incertidumbre en los análisis de ingeniería geotécnica. Los resultados de las pruebas de laboratorio sobre los suelos naturales, indican que la mayoría de las propiedades del suelo pueden ser consideradas como variables aleatorias que se ajustan a la función de distribución normal. 

Cuantificación de Incertidumbres en las Propiedades del Suelo

Las propiedades in situ del suelo puede variar verticalmente y horizontalmente por una variedad de razones, incluyendo:

• Ambiente de sedimentación: En general, los suelos de grano fino se depositan en ambientes de baja energía, y por tanto son más uniformes que los suelos de grano grueso, que suelen ser depositados en ambientes de alta energía (flujos, avalanchas, avenidas, etc.).
• Grado de meteorización: Las propiedades del suelo puede ser influenciadas por el intemperismo, un factor que afecta el suelo en la superficie del terreno más fuertemente, y que disminuye con la profundidad bajo la superficie del suelo. Sin embargo, factores como la erosión y las tasas variables de deposición locales, pueden producir perfiles de suelo con efectos variables de meteorización.
• Entorno físico: La mayoría de los suelos presentan propiedades, tales como anisotropía intrínseca e inducida, que son influenciadas por su entorno físico. Debido a los cambios de esfuerzos que se pueden producir localmente durante la vida de un depósito de suelo, sus efectos pueden introducir incertidumbre en las propiedades medidas del suelo.

La variación espacial de las propiedades del suelo se compone de varios componentes y se puede representar mediante un modelo simple (propuesto por Phoon y Kulhawy, 1999):

x(z) = t(z) + w(z) + e(z)

donde:

ξ = propiedad del suelo in situ,
t = componente de tendencia determinista,
w = componente aleatorio,
e = error de medición, y
z = profundidad.

Los componentes de tendencia y aleatorio de la variación espacial en las propiedades del suelo, se ilustran gráficamente en la siguiente figura.

Variabilidad inherente del suelo (Phoon & Kulhawy, 1999)

Los principios básicos de la mecánica de suelos indican que muchas de las propiedades de interés del suelo, están altamente influenciadas por la presión de confinamiento efectiva, y debido a que estos esfuerzos generalmente aumentan con la profundidad, es de esperarse que estas propiedades exhiban alguna tendencia regular y predecible con la profundidad. La tendencia se puede determinar mediante el ajuste (en un sentido de mínimos cuadrados) de una función determinista suave (smooth) (por ejemplo, una línea recta, parábola o exponencial) de los datos o por un procedimiento de media móvil.

El componente aleatorio de la variabilidad del suelo también se conoce como "variabilidad inherente del suelo", que se expresa con respecto a la tendencia determinística de la propiedad, como se ilustra en la figura anterior.

El error de medición, ya sea a partir de mediciones de laboratorio o de campo, puede introducir variabilidad adicional en las propiedades del suelo. El error de medición puede surgir de equipo, el operador y los efectos aleatorios de las pruebas (Phoon y Kulhawy, 1999 en "Characterization of geotechnical variability", Canadian Geotechnical Journal, Vol. 36, pp. 625-639.).

La escala de fluctuación es un término que describe la variación espacial de la propiedad de interés respecto de la tendencia (como se muestra en la figura anterior). Un parámetro con una escala corta de fluctuación cambia rápidamente con la posición, uno con una gran escala de fluctuación cambia en grandes distancias. 

El Coeficiente de Variación COV y la variabilidad inherente del suelo

El coeficiente de variación COV representa una medida relativa (y adimensional) de la dispersión de un conjunto de datos, y se expresa como:

El COV ha sido comúnmente utilizado para describir la variación de muchas propiedades geotécnicas del suelo y parámetros de prueba in situ. Se debe tener en cuenta que la media, la desviación estándar, y el COV son interdependientes - y conociendo dos de éstos parámetros, se obtendrá el tercero.

En la práctica, resulta conveniente estimar los momentos de los parámetros geotécnicos del suelo, donde hay pocos datos disponibles (datos parciales), suponiendo que el COV es similar a los valores previamente medidos de otros conjuntos de datos del mismo parámetro.

La dispersión de la escasez de datos también puede estimarse utilizando otros métodos tales como la "regla de 3 sigma". Este método de aproximación de la varianza reconoce que el 99,73% de todos los valores de un parámetro normalmente distribuido, están dentro de tres desviaciones estándar del promedio.

De acuerdo con la regla de 3 sigma, las desviaciones estándar se pueden aproximar dividiendo el rango (el valor más alto menos el valor más bajo) por 6. Duncan (2000) señala que los ingenieros tienen una tendencia a subestimar el intervalo entre los valores mínimos y máximos concebibles, por lo tanto, debe hacerse un esfuerzo conciente para hacer el intervalo entre los dos tan alto como sea posible. Christian et al. (2001) también advierten que los ingenieros con menos experiencia en la estadística calcularán los valores mínimos y máximos concebibles con un sesgo (desviación) significativo, poco conservador. El campo de las estadísticas de orden ofrece una alternativa a la regla de 3 sigma que considera la cantidad de datos disponibles.

En las siguientes tablas, se presentan los valores de COV para diferentes propiedades y parámetros del suelo, que evidencian su variabilidad inherente:

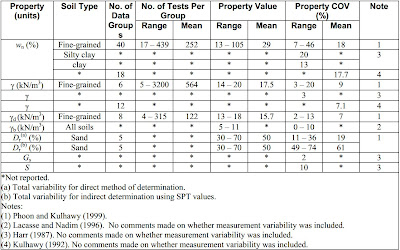COV de variabilidad inherente del suelo para humedad, peso unitario y densidad relativa 

COV de variabilidad inherente del suelo para Límites de Atterberg 

COV de variabilidad inherente del suelo para propiedades de resistencia

COV de variabilidad inherente del suelo para consolidación y permeabilidad

La Evaluación del Riesgo

Según Whitman (2000), la Evaluación del Riesgo es el proceso de obtener un Riesgo Cuantificado, que puede ser calculado mediante cualquiera de los siguientes métodos:

1. La teoría y los cálculos numéricos o 
2. Mediante juicios subjetivos.

La Evaluación del Riesgo es más amplia. Incluye la identificación de amenazas, riesgos y consecuencias; la investigación de las posibles medidas para reducir los riesgos y las consecuencias, y la priorización de las acciones correctivas. La Evaluación del Riesgo puede o no puede implicar la cuantificación de los riesgos.

Las siguientes medidas son recomendadas por la Sociedad Americana de Ingenieros Civiles (1997) para reducir los riesgos geológicos:

• Proveer un presupuesto adecuado para explorar las condiciones del subsuelo.
• Mantener consultores de diseño debidamente cualificados y con experiencia para investigar, evaluar los riesgos potenciales, preparar planos, especificaciones y un Informe Geotécnico de Base (Geotechnical Baseline Report) consistente con los riesgos.
• Asignar tiempo y recursos financieros suficientes para preparar un claro Informe Geotécnico de Base que sea coherente con los documentos de diseño.
• Desarrollar provisiones para pago por precios unitarios que se puedan ajustar a las condiciones encontradas.
• Revisar y discutir las líneas de base con los oferentes antes de que las ofertas sean presentadas. Se recomienda que esto se haga en un taller previo a la licitación después de pre-calificación.
• Mantener un fondo de reserva correspondiente, en función de los riesgos percibidos del proyecto.

Los riesgos geotécnicos, en forma de condiciones geológicas imprevistas, son un factor importante en el costo y el control cronológico en todos los proyectos de ingeniería civil más importantes. Las cantidades de dinero, involucradas en las reclamaciones derivadas de estos problemas geotécnicos, es enorme y debe ser tomada muy en serio por los organismos de financiación y las organizaciones de ingeniería.

Las investigaciones inadecuadas de sitio se clasifican como uno de los principales contribuyentes al riesgo geotécnico. Asignaciones más realistas de tiempo y dinero tienen que hacerse a estos programas de investigación de sitio. También es importante que los ingenieros geólogos y geotécnicos hagan un uso más eficiente de los recursos asignados a la investigación de sitio. Los tradicionales pozos verticales pueden no ser adecuados para definir las condiciones en un sitio geológicamente complejo y debe hacerse un uso innovador de pozos horizontales y túneles de exploración. La investigación en curso durante la construcción, también es importante y perforaciones de sondeo, adelante del frente de excavación de túneles o la colocación de dispositivos sísmicos de predicción, adelante de máquinas tuneladoras, pueden ayudar a definir las dificultades antes de que sean encontradas.

El empleo de consultores experimentados en la etapa inicial de un proyecto también puede contribuir a la reducción de los riesgos geológicos y geotécnicos. El juicio de estas personas, construido sobre su amplia experiencia en entornos geológicos similares, puede ayudar a poner los problemas en perspectiva y establecer prioridades para el uso de los limitados recursos y tiempo.

Procedimiento para la determinación del riesgo geotécnico en túneles

La variación en los parámetros del suelo

El uso del análisis de confiabilidad en la Ingeniería Geotécnica, a veces referido como el método probabilístico, ha recibido la aprobación por parte de muchos investigadores geotécnicos desde la publicación pionera de Lumb en la década de 1960s (Lumb 1966, 1967, 1968). 

El factor de seguridad FOS, no es una buena medida de la probabilidad de falla en la Ingeniería Geotécnica. Un sistema geotécnico con un mayor factor de seguridad puede tener una mayor probabilidad de falla que uno similar diseñado para un factor de seguridad más bajo. La relación entre la probabilidad de falla y el factor de seguridad depende de la confiabilidad del modelo de diseño y de las incertidumbres de los parámetros geotécnicos de entrada.

Debido al esfuerzo de innumerables investigadores,  se han alcanzado avances significativos en el análisis de la confiabilidad en la ingeniería geotécnica. Esfuerzos excepcionales también se han dirigido hacia el desarrollo de una nueva generación de códigos geotécnicos respaldados por análisis de confiabilidad. Desde hace mucho tiempo las figuras prominentes en el campo determinista han comenzado a apoyar o aceptar un mayor uso de métodos de confiabilidad en la Ingeniería Geotécnica.

Sin embargo, el objetivo inmediato de convencer a los ingenieros en ejercicio de adoptar el diseño basado en la confiabilidad, sigue siendo un desafío. La mayoría de los ingenieros geotécnicos pueden no tener una sólida formación en las matemáticas de análisis de confiabilidad. Es necesario aclarar a los ingenieros geotécnicos el vínculo entre el análisis matemático algo abstracto, y los problemas reales de ingeniería, y  demostrarles que el análisis de confiabilidad puede producir resultados realistas y significativos.

Cualquier forma de análisis de confiabilidad requiere por lo menos dos parámetros probabilísticos: la media y la varianza, señalando que la varianza es cuadrado de la desviación estándar. 

Importancia del Juicio de Ingeniería

Hay una gran cantidad de trabajos que se enfocan en el desarrollo de análisis de confiabilidad cada vez más complejos. Sin embargo, a los ingenieros geotécnicos les puede resultar más difícil llegar a entender los complejos conceptos probabilísticos y la terminología. Esto conduce a una no poco común percepción de que la mayoría de los artículo sobre el diseño basado en la confiabilidad, sugieren la aplicación ciega de análisis estadístico sin una entrada (de análisis) adecuada de los criterios de juicio de ingeniería. En el campo determinista es frecuente el uso de criterios análisis de entrada, basados en el juicio de ingeniería.

El análisis de confiabilidad no es un sustituto del juicio de ingeniería o cualquier otra herramienta geotécnica, y tampoco de los avances logrados fuera del mundo de la confiabilidad (estadística). El juicio de ingeniería es, de hecho, consagrado en el análisis de confiabilidad en dos formas: La probabilidad bayesiana y los valores críticos de juicio.

En la probabilidad Bayesiana, la experiencia o el juicio de un ingeniero es el antecedente. Esta experiencia o juicio se puede combinar con datos específicos del sitio o del proyecto en el marco teórico de la probabilidad Bayesiana, para producir un valor actualizado de la probabilidad como tratan muchos libros clásicos sobre los métodos probabilísticos, por ejemplo Ang y Tang (1984).

Los valores de juicio son utilizados (y de hecho son necesarios) cuando sólo se dispone de pocos datos para una propiedad del suelo al azar, en particular. Esto es algo esperado, ya que obtener de forma determinista una propiedad del suelo adecuada, es un reto. La incertidumbre en un valor crítico de juicio, es similar en concepto a la de la incertidumbre en el muestreo, y por lo tanto puede ser tratada de una manera similar. También es evidente que, con el fin de reducir la incertidumbre en los valores críticos de juicio, la asignación de valores de juicio debe llevarla a cabo los ingenieros experimentados. El valor de entrada de juicio (judgemental) en un análisis de confiabilidad se relacionaa con las incertidumbres y la falta de datos, de una manera es más transparente. Siempre es trazable a un componente específico del proceso de diseño, y su efecto se puede evaluar objetivamente dentro de un marco teórico.

Esto se considera superior en jerarquía, a un proceso difuso de selección de un mayor o menor factor de seguridad, en un intento por explicar algunas incertidumbres mal definidas, distribuidas en los diversos componentes del diseño; de manera difusa.

Valor puntual vs Promedio espacial

Una propiedad del suelo es considerada como de variabilidad espacial aleatoria, en la medida en que  los valores reales (es decir, hallazgos) de las propiedades del suelo, pueden variar de un punto a otro, dentro de una masa de suelo aparentemente homogénea.

Las propiedades probabilísticas de una propiedad del suelo en un punto particular (que se denomina propiedad del punto por Li y Lumb, 1987) puede ser caracterizada por un valor medio y una varianza Var{X}.

Esta variabilidad de punto a punto se conoce como variabilidad innata o variabilidad espacial (Vanmarcke 1977, Li y Lee 1991). Para la condición ideal de prueba perfecta, la variabilidad de un parámetro X del suelo, obtenida a partir del ensayo de diferentes muestras, se debe únicamente a la variabilidad innata.

Como lo discuten Li y Lumb (1987), Li (1991, 1992) y Li y Lee (1991), la varianza apropiada para ser utilizada para los análisis probabilísticos, puede no ser necesariamente ser la de propiedad del punto.

La influencia de la variabilidad innata en un problema de estabilidad puede ser ilustrada por un problema de estabilidad de taludes ideal, como se ilustra en la siguiente figura. 

Variabilidad innata y promedio espacial

La idealización del material comprende un material de cohesión constante, por ejemplo, X es la cohesión. La distancia curvilínea a lo largo de la superficie de falla potencial se denota como v. El valor de cohesión tiene una media de población cμ. La variabilidad innata de X se indica por la línea en zigzag. La que gobierna la inestabilidad del talud es la "cohesión promedio a lo largo de la superficie potencial de falla".

En aras de la simplicidad en la discusión, consideremos el caso ideal de tener "n" elementos idénticos pero independientes a lo largo de la superficie de deslizamiento. La resistencia del i-ésimo elemento, está dada por Xil, donde Xi y L son la propiedad y la longitud del elemento i-ésimo. La resistencia total, R, viene dada por

(ΣXi)/n es el valor medio a lo largo de la trayectoria de falla. Puesto que la pendiente se considera estadísticamente homogénea, Var {ΣXi/n} = {Var ΣX/n}. A medida que los elementos se consideran estadísticamente independientes, la ecuación para calcular la varianza de ΣX/n, como se presenta en muchos libros elementales de texto sobre probabilidad, es simplemente: Var {ΣX/n} = Var {X}/n. Esto significa que la varianza de R, que es controlada por la variación del valor promedio de X, es reducida por un factor de 1/n.

En realidad, no se puede simplemente dividir los elementos del suelo a lo largo de la superficie de falla (o dominio) en un número de elementos independientes estadísticamente. Las propiedades del suelo en diferentes ubicaciones están de algún modo correlacionadas. Sin embargo, la propiedad media de X a lo largo de un dominio (superficie) de falla determinado, denotado como X, se reduce siempre con relación a ese X. Esto se indica en  la zona sombreada de la figura anterior.

Esta reducción puede modelarse matemáticamente usando el Modelo de Campo Aleatorio de Vanmarcke (1977), y se puede expresar como:

donde Var {X} denota la varianza de una variable aleatoria, y Γ² se conoce como el factor de reducción de la varianza debido a que su valor es siempre menor que la unidad. El valor de Γ es dependiente del tamaño del dominio de falla y la escala de fluctuación, δ, siendo esta última un parámetro del Modelo de Campo Aleatorio (Vanmarcke 1977, Li y Lee 1991). Recordando que la desviación estándar es la raíz cuadrada de la varianza, la ecuación (2) se puede reescribir como:

Donde σ{X} Denota la desviación estándar de una variable aleatoria. Esta situación es análoga a la de los resultados de los exámenes de los estudiantes que se correlacionan. Aunque la puntuación de un estudiante individual puede manifestar una dispersión significativa del promedio anual, la puntuación media de un grupo de estudiantes manifiesta una dispersión significativamente menor.

La evaluación de Γ, en general, es complicada. Si el dominio de falla puede ser caracterizado por una dimensión L, y bajo la condición de L ≥ 2δ, la siguiente ecuación aproximada se puede utilizar (Vanmarcke 1977, Li y Lee 1991).

En general, un estrato de suelo "menos variable" tiene un valor más alto de δ. Los datos de Lumb (1975) de arcilla marina en Hong Kong dieron δ <1 m, y esto fue apoyado por más datos reportados en Li (1989). Los datos de Day (1993) para un depósito de limo en Canberra dieron δ de ~ 1,2 m.

Es evidente a partir de las ecuaciones (2) a (3) que si la varianza (o desviación estándar) de X se toma  erróneamente se toma como X, entonces la variabilidad (o incertidumbre) de los parámetros que rigen la ocurrencia del estado límite será sobre-estimada.

En el cálculo del factor de reducción de la varianza, la determinación de un dominio de falla apropiado, basado en consideraciones de ingeniería es un requisito a priori. En un problema de estabilidad de taludes controlado por un contacto débil, el geo-parámetro correspondiente X debe ser la resistencia promedio a lo largo de la trayectoria de falla en este contacto débil. La población correspondiente es todo el contacto débil y no el el del talud. De nuevo, esto pone de relieve la importancia de los criterios de sana ingeniería en un análisis de confiabilidad.

Referencias:

• Andreas, Goricki, Jürgen, Schick K. y Arnold, Steidl. Quantification of the Geotechnical and Economic Risk in Tunnelling. Graz University of Technology.
• Ang, A.H.S. Tang, W.H. 1984.  Probabilistic concepts in engineering planning and design.  John Wiley & Sons, Sydney, 1975.  
• Hoek, Evert y Palmeiri, Alessandro  Geotechnical risks on large civil engineering projects. Keynote address for Theme I – International Association of Engineering Geologists Congress, Vancouver, Canada, September 21 to 25, 1998
• Jones, Allen L., Kramer, Steven L. y Arduino, Pedro. Estimation of Uncertainty inGeotechnical Properties for Performance-Based Earthquake Engineering. PEER Report 2002/16. Pacific Earthquake Engineering Research Center. College of Engineering. University of California, Berkeley. December 2002.
• Li, K. S. &  Lo, S.R. Variance of soil parameters: some common misconceptions. TAIPEI 2006. International Symposium on New Generation Design Codes for Geotechnical Engineering Practice. Nov. 2~3, 2006, Taipei, Taiwan.
• Lumb, P. 1966.  The variability of natural soils.  Canadian Geotechnical Journal, 3, 74-97. 
• Lumb, P. 1967.  Statistical methods in soil investigations.  Proc. 5th  Australian-New Zealand Conference on Soil Mechanics and Foundation Engineering, 26-33. 
• Lumb, P. 1968. Statistical aspects of soil measurements.  Proc. 4th  Australian Road Research Conference, 4, 1761-1770.
• Whitman, Robert V. Organizing and Evaluating Uncertainty in Geotechnical Engineering. Journal of Geotechnical and Geoenvironmental Engineering. July 2000.

Guardar en PDF