 |
| Portada |
 |
| Escalera Noble. Real Academia de Ingeniería |
Respetuosamente, se transcriben a continuación, algunos apartes del discurso inaugural de la Real Academía de Ingeniería, leído en Madrid en el año 2005, por parte del Doctor Ingeniero de Caminos Eduardo Alonso Pérez de Ágreda, por considerarlos fundamentales en la comprensión de la evolución de la Ingeniería geotécnica, tema que se ha venido desarrollando de manera detallada en numerosos capítulos de "Apuntes de Geotecnia con Énfasis en Laderas" y que, con este material se ve enriquecido.
 |
| Eduardo Alonso Pérez de Ágreda |
Algunos de los importantes documentos de Eduardo Alonso Pérez de Ágreda, pueden ser consultados en el Servei de Biblioteques i Documentació, de la Universitat Politècnica de Catalunya.
La larga y rica vinculación de la Geotecnia a la historia de la construcción de obras y la dificultad para sistematizar y entender el comportamiento de una variadísima gama de materiales (todos los presentes en el medio geológico) han introducido una carga empírica fuerte en sus manifestaciones, incluso en los desarrollos teóricos y conceptuales. El progreso de la Geotecnia se beneficia de ese contacto estrecho con el mundo práctico, que es uno de sus pilares fundamentales. Los otros dos son, seguramente, la experimentación en laboratorio e “in situ” y el desarrollo de marcos conceptuales, teorías y modelos. El equilibrio requiere los tres apoyos. En otras palabras, es difícil dominar el arte de la Geotecnia sin una formación adecuada en esos aspectos, que lógicamente están densamente relacionados.
Ello no es óbice para que se
puedan desarrollar meritorias carreras, profesionales o académicas, en uno solo
de los pilares mencionados. Pero ello exige una buena dosis de habilidad o de
virtuosismo. Falta, por último, recordar la gran influencia de una poderosa
ciencia que interpreta el medio geológico, la Geología. La integración de todo
ello es tarea de muy pocos y conduce a la excelencia.Viene a la cabeza aquí la
vida y contribuciones de K. Terzaghi, considerado el fundador de la Mecánica
del Suelo, que supo aglutinar los pilares geotécnicos con insuperable maestría.
1. Primer paradigma. Ley de resistencia al esfuerzo cortante de
Coulomb. C.A. Coulomb (Angoulême 1736 – París 1806)
Charles-Augustin Coulomb se graduó en el Cuerpo Militar de Ingenieros de Francia en 1761 y uno de
sus primeros trabajos fue la construcción del Fuerte Bourbon en La Martinica.
Sus experiencias en ese puesto (hasta 1772) fueron decisivas en el análisis que
hizo de los empujes sobre muros en su famoso ensayo (presentado a la Academia
de Ciencias de Paris, en 1773), “Sur une application des règles de
maximis et minimis à quelques problèmes de statique relatifs à l’architecture”.
La teoría de empuje de tierras a partir del equilibrio estático de cuñas,
desarrollada por Coulomb, se enseña hoy en los cursos introductorios de
Geotecnia. Es en ese ensayo donde propone explícitamente que la resistencia (al
esfuerzo cortante decimos ahora) opuesta por un plano a deslizar tenga dos
contribuciones: un término constante, que él denomina “cohérence” δ, (hoy
descrita como cohesión, c) y otro proporcional a la fuerza normal al plano en
cuestión o fricción (que lo expresa con la notación 1/n, aunque hoy utilizamos
el concepto de ángulo de fricción, de forma que el coeficiente lo escribimos
como tan ϕ).
 |
| Mapa de la isla de Martinica (Antillas Francesas) |
 |
| Localización del Fuerte Bourbon |
 |
| Fuerte Bourbon (según las reglas de Vauban) |
En el caso
de la fricción, Coulomb acepta las conclusiones de los estudios previos de
Amonton. Coulomb siguió involucrado en problemas de ingeniería de construcción
hasta 1781, año en que fue elegido miembro de la Academia de Ciencias. Su
segunda contribución importante a la mecánica fue su investigación sobre las
leyes de la fricción entre materiales. El resto de sus contribuciones, las más
conocidas, pertenecen ya a la Física, donde fundó los principios de la
electroestática. Probablemente Coulomb llegó a la conclusión de que la
estabilidad de muros estaba ligada a la estabilidad de un cuerpo compuesto por
el propio muro y una cuña de tierras adosada a él, a partir de sus
observaciones de roturas en el transcurso de su trabajo en el Fuerte Bourbon.
Se trata seguramente de roturas como la representada en la Figura 'Falla de muro de contención', que en
este caso corresponden a otro fuerte de imponentes dimensiones: la ciudadela de
Lleida. Coulomb trasladó estas observaciones al esquema de la Figura 'Esquema utilizado por Coulomb para derivar el empuje activo y pasivo', que
fue el que utilizó para razonar su teoría a partir de la búsqueda de valores
máximos y mínimos de los empujes sobre el muro asociados a una geometría
genérica de la cuña (la CBa o CB’a’ de la Fig.
'Esquema utilizado por Coulomb para derivar el empuje activo y pasivo'). La ley de rotura de
Coulomb, con nomenclatura moderna, se escribe:
τf = c + σ tan ϕ
donde τf es la resistencia a
esfuerzo cortante disponible por unidad de área de un plano del interior de la
masa de suelo sometida a una tensión normal de intensidad σ. Los parámetros c y
ϕ serían constantes para
un suelo determinado.
Esta ley de rotura es la piedra
angular de los estudios de estabilidad. Su origen es experimental pero está
ligado también a la observación de la rotura de muros, una pequeña catástrofe
si se compara con otras examinadas aquí, pero que correctamente interpretada
permitió establecer un primer paradigma de la Mecánica del Suelo.
 |
| Esquema utilizado por Coulomb para derivar el empuje activo y pasivo |
 |
| Presión activa de Coulomb. Caso c=0 |
La Estabilidad de Taludes
El cálculo de las condiciones de
estabilidad de taludes fue uno de los primeros desarrollos, en los comienzos
del siglo XX, de la naciente teoría de la Mecánica del Suelo. Se atribuye a
K.E. Petterson la propuesta del denominado “método sueco” para el análisis de
la estabilidad de taludes uniformes mediante superficies de rotura circulares.
Petterson estudió la rotura de un muelle de carga en Göteborg en el año 1915 o
1916. Una aportación significativa de su estudio y del que llevó a cabo la
Swedish Geotechnical Comission en los años 1920-1922 fue la determinación de la
forma de la superficie de rotura. Se concluyó que las formas circulares se
ajustaban bien a la realidad. El método de Petterson estuvo en boga en los años
1930-1940.
Terzaghi (1936) lo describe con ayuda de la Figura 'Esquema para la aplicación del método de K.E. Petterson. Terzaghi (1936)'. Se introduce el concepto de Factor de Seguridad (FS), S, como cociente de dos momentos: el de las tensiones de corte resistentes a lo largo de la superficie de rotura AC y el del peso de la masa potencialmente inestable ABC, limitada por el propio talud y por la superficie circular supuesta de rotura. Con la notación utilizada por Terzaghi:
.jpg) |
| Falla del muelle de Gothenbur en 1916 |
 |
| Método sueco de falla circular |
Terzaghi (1936) lo describe con ayuda de la Figura 'Esquema para la aplicación del método de K.E. Petterson. Terzaghi (1936)'. Se introduce el concepto de Factor de Seguridad (FS), S, como cociente de dos momentos: el de las tensiones de corte resistentes a lo largo de la superficie de rotura AC y el del peso de la masa potencialmente inestable ABC, limitada por el propio talud y por la superficie circular supuesta de rotura. Con la notación utilizada por Terzaghi:
La masa deslizante se divide en n
elementos o “columnas” de anchura Δl. La resistencia al corte que ofrece el
suelo se calcula con la ley ya descrita de Coulomb (con los parámetros de
cohesión, c, y ángulo de fricción, ϕ).
La ecuación proporciona un valor numérico para S, si se conoce la
superficie de rotura. El FS cambiará al variar esas superficies. El valor
mínimo de S entre todas las superficies posibles se puede considerar como una
estimación razonable del factor de seguridad del talud.
Uno de los primeros ensayos que
se pusieron a punto con objeto de determinar c y ϕ
fue el denominado ensayo de “corte directo” que trataba de reproducir las
condiciones tensionales de un elemento de una superficie de rotura como la
indicada en la Figura
'Esquema para la aplicación del método de K.E. Petterson. Terzaghi (1936)' . Sigue siendo un equipo habitual en todos los
laboratorios de Geotecnia.
2. Segundo paradigma. Ley de la tensión efectiva de Terzaghi. Karl von Terzaghi (Praga 1883 – Winchester 1963)
En el período 1913 a 1934, dos
profesores de la Universidad Técnica de Viena, P. Fillunger y K. Terzaghi,
desarrollaron una intensa investigación sobre determinados aspectos del
comportamiento de sólidos porosos saturados. Uno de ellos, la cuestión de la
“subpresión” (“uplift pressure”) en presas de fábrica
(Figura 1.10) era fundamental para la determinación de la seguridad de estas
estructuras y fue el origen del primer enfrentamiento entre Fillunger y
Terzaghi.
 |
| Esquema utilizado por Fillunger para discutir el problema de la subpresión en presas. Según R. de Boer (1999) |
En 1923 Terzaghi derivó la ecuación diferencial de la consolidación
de suelos saturados (una derivación que R. de Boer, 1999 califica de “oscura en
parte”). En 1925 publicó Erdbaumechanik auf Bodenphysikalischer
Grundlage, un libro con soluciones teóricas para una serie de problemas
prácticos de la Geotecnia. En 1936, conjuntamente con O.K. Frölich, escribe un
libro sobre la teoría de la consolidación en el que se describe la solución
analítica al problema de la consolidación y se relacionan los asientos del
suelo saturado con la disipación de las presiones intersticiales. Esta
publicación fue objeto de una dura disputa entre K. Terzaghi y P. Fillunger,
que acabó con el suicidio de este último en Viena, en 1937. En todos estos
trabajos, la cuestión del efecto de la presión de agua en el comportamiento del
suelo saturado estuvo presente de una forma u otra. Sin embargo, su importancia
decisiva en aspectos como la resistencia al esfuerzo cortante tardó en
entenderse de manera precisa. No fue hasta 1936 que el principio de las
tensiones efectivas fue formulado claramente por Terzaghi.
Una consecuencia inmediata de
este principio es que la formulación de la resistencia a esfuerzo cortante
disponible en un plano a través del suelo (Coulomb) debe escribirse con más
generalidad como:
τ = c’ + σ’ tan ϕ’ = c’ + (σ - u) tan ϕ’
donde la tensión normal se
convierte en efectiva (σ’). Los parámetros de resistencia de Coulomb se
designan ahora c’ y ϕ’
para destacar que corresponden a la formulación de la resistencia en tensiones
efectivas. La influencia del agua en la estabilidad de taludes quedaba así
claramente establecida. El efecto del agua estaba asociado a su presión y no a
un supuesto efecto lubricante.
Asentamientos diferidos
El concepto de “tensión efectiva”
desarrollado por Terzaghi en el período 1923-1936 le permitió desarrollar la
teoría de la consolidación, que explica el asiento diferido de estratos de
arcilla saturada, sometidos a carga. La idea fundamental es que el desarrollo
de asientos en el tiempo se explica por el flujo de agua que escapa del estrato
en cuestión.
El agua de los poros,
prácticamente incompresible, recibe inicialmente la carga transmitida por la
tensión exterior. Pero inmediatamente se generan gradientes de presión desde el
interior del estrato hacia los contornos si es que se permite en ellos el
drenaje, como es habitualmente el caso. Terzaghi y Peck (1948) incluyeron en su
libro Soil Mechanics in Engineering Practice el esquema que se reproduce en la
Figura 3.1 para explicar este proceso. El estrato arcilloso se concibe como una
colección de tabiques horizontales perforados, separados por muelles. En los
extremos el agua puede drenar libremente. La carga exterior, aplicada
rápidamente, se transmite al agua que satura el espacio entre tabiques. Pero
inmediatamente la cámara extrema del apilamiento puede descargar agua hacia el
exterior, a través de los orificios del tabique superior que quieren simular la
permeabilidad del suelo. La pérdida de volumen de la primera celda se traduce
en la carga de los muelles. El equilibrio de tensiones en planos horizontales
debe cumplirse siempre, es decir, que la tensión total exterior será la suma de
la presión de agua y de la carga que reciban los muelles. De acuerdo con el
principio de tensiones efectivos, la carga que reciben los muelles representa
la tensión efectiva en la celda correspondiente.
El proceso descrito penetra hacia
el interior del apilamiento de tabiques y muelles a medida que el agua fluye
hacia el exterior. En la medida en que los orificios de los tabiques sean
pequeños, es decir, en la medida en que la permeabilidad sea pequeña, el
proceso de deformación se retardará. Terzaghi encontró que la función
que describe la presión de agua en un punto de ordenada z, en el tiempo t, era
la solución de una ecuación diferencial parabólica:
donde u(z, t) es la presión
intersticial y cv, una constante del material.
Terzaghi la resolvió en 1935 con
ayuda del matemático O.K. Frölich. Conjuntamente publicaron en 1936 el libro
Theorie der Setzung von Tonschichten (Teoría del asiento de capas de arcilla).
Este libro fue duramente criticado por P. Fillunger, profesor de Mecánica de la
Universidad Técnica de Viena. La acusación de Fillunger no fue únicamente
técnica, sino que introdujo ataques personales y difamatorios contra Terzaghi y
Frölich. La disputa acabó trágicamente unos meses después, en marzo de 1937,
con el suicidio de P. Fillunger y su mujer.
El análisis de la consolidación
por Terzaghi fue la clave para entender los asientos a largo plazo de
estructuras cimentadas sobre suelos arcillosos. Entre los suelos arcillosos,
los de alta deformabilidad han planteado problemas de gran envergadura a la
comunidad geotécnica.
Se han elegido dos casos
espectaculares y bien conocidos para ilustrar la dificultad de cimentar sobre
ellos: la Catedral Metropolitana de México DF y la Torre de Pisa.
3. Tercer paradigma: el estado
crítico
En 1968 se publican dos libros de
texto que estaban destinados a tener una gran difusión en las universidades de
todo el mundo que incluían la Mecánica del Suelo en sus programas de enseñanza:
Soil mechanics, de T.W. Lambe y R.V. Whitman, y Critical state soil mechanics,
de A. Schofield y P. Wroth. A pesar de los objetivos modestos que
anuncian sus autores en los prefacios, no cabe duda de que estaban concebidos para
proporcionar un edificio teórico completo de la Mecánica del Suelo,
especialmente en sus conceptos básicos. Los dos libros tratan fundamentalmente
del comportamiento del suelo y más concretamente de las relaciones
tensión-deformación. Lambe y Whitman eran entonces profesores de Mecánica del
Suelo en el MIT, en Boston. Por su parte, Schofield y Wroth eran “lecturers” en
la Universidad de Cambridge. Los dos centros disfrutaban de una gran reputación
en Ingeniería Civil. Un examen del índice de ambos textos revela sus
diferencias.
Los autores centran la estructura
de la Mecánica del Suelo en torno al papel del agua intersticial (Partes III,
IV y V (última)). Dentro de cada una de ellas mantienen las ideas clásicas de
Terzaghi centradas en discutir como entes bastante independientes la
resistencia y las relaciones tensión-deformación. Los conceptos drenado y no
drenado requieren una explicación “ad hoc” como también la requiere el concepto
de resistencia no drenada que se ha descrito más arriba. El libro de Schofield
y Wroth parece que aborda otra materia.
¿Qué es eso de Granta-gravel y
Cam-clay? El río Cam pasa por Cambridge y el arroyo Grant es un pequeño curso tributario
del Cam. Los autores eligieron los nombres de esos ríos para construir dos
materiales imaginarios. El que se hizo con el tiempo universalmente conocido (y
aplicado) fue Cam-clay (especialmente su versión modificada). En el año 1969
otro profesor de Cambridge, C.R. Calladine, perteneciente también al
departamento de ingeniería, había publicado un pequeño libro: Engineering
plasticity. Allí no se hablaba de suelos, pero sí de materiales
estructurales y de fundamentos de la plasticidad, entre ellos de la “regla de
la normalidad”. Aparentemente fue Calladine quien sugirió a Schofield y Wroth
la conveniencia de utilizar la plasticidad rigidizable como marco general para
construir modelos constitutivos de suelos. Los cierto es que, en una desviación
fundamental de lo que había sido hasta ese momento la escuela de pensamiento en
Mecánica del Suelo, los autores “derivaron” modelos constitutivos sencillos que
se podían parecer a alguna clase de suelos (materiales remoldeados, libres de
una estructura microscópica complicada) extensamente ensayados en el
laboratorio.
La constante, C, define el tamaño
de la superficie de fluencia, es decir, la extensión del dominio elástico.
Parece lógico relacionar este tamaño con la densidad del suelo. Así, la constante,
C, se hizo depender de las deformaciones volumétricas plásticas, y esta
dependencia introduce los parámetros de compresibilidad en el modelo, que queda
así completo.
A partir de aquí es posible
generar respuestas de este suelo ideal cuando es sometido a trayectorias
tensionales arbitrarias. El modelo incorpora, de forma natural, en una
formulación unitaria, propiedades que se pueden considerar representativas de
la rigidez (la constante C que introduce la compresibilidad) con otras propias
del estado último o en rotura (el coeficiente M de la presentación anterior).
Este hecho supone un cambio profundo si se compara con la Mecánica del Suelo
clásica, descrita en los textos de Terzaghi y Peck (1948) y de Lambe y Whitman
(1968). La resistencia “no drenada”, un concepto que tradicionalmente requería
una explicación “ad hoc”, relacionada con la generación de presiones
intersticiales, es simplemente una respuesta natural de Cam-clay frente a una
trayectoria particular: la que se produce a volumen constante. La comprensión
unificada del comportamiento del suelo que introdujo este modelo es su gran
aportación a la Mecánica del Suelo.
El desarrollo de los conceptos de
estado crítico condujo a la aparición rápida de modelos progresivamente más
perfeccionados, casi siempre dentro del “paraguas” de la plasticidad. Este
desarrollo, que sigue en curso, tuvo inicialmente poco impacto sobre la
ingeniería, es decir, sobre los problemas fundamentales de diseño y
construcción geotécnica. Sin embargo, la aparición de programas de cálculo
geotécnico de utilidad general hace una década supuso un cambio progresivo
hacia la utilización de modelos sofisticados en problemas aplicados. Hoy es
difícil encontrar una consultoría geotécnica que no utilice sistemáticamente
esos programas. En ellos, los modelos de estado crítico y sus derivados son la
opción más habitual para una representación “avanzada” del suelo.
Con la perspectiva de hoy (2005),
el texto de Lambe y Whitman (1968) pertenecía ya al pasado de la Mecánica del
Suelo. El texto de Schofield y Wroth (1968) abría una nueva época.
Otros enlaces importantes y recomendados sobre el tema en este blog:
- Terzaghi y el Método Observacional
- La Consolidación de la Mecánica de Suelos: 1920-1970 por Ralph B. Peck
- Terzaghi y la Mecánica de Suelos
- El Legado de Terzaghi en la Ingeniería Geotécnica
- El Ascenso de la Geotecnia en 1936
- La Clasificación Geomecánica de Terzaghi (1946)
- Precursores de la Ingeniería Geotécnica
- Terzaghi el ingeniero y el escándalo Fillunger
- Terzaghi y el SPT
- La Consolidación de la Mecánica de Suelos: 1920-1970 por Ralph B. Peck
- La Ingeniería Geotécnica
- Citas Destacadas de Terzaghi
- Terzaghi y el Diseño Racional




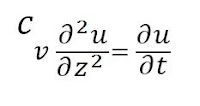

Gracias es excelente ayuda, muchas gracias
ResponderBorrar